262 El Teorema de Fubini-Tonelli 26.1 La demostraci´on del teorema general puede reducirse al caso particular en que f = XE, la funci´on caracter´ıstica de un conjunto medible, utilizando el siguiente hecho: 26.2 (a) Si una funci´on f ‚ 0 satisface el teorema de Tonelli, entonces tambi´en lo satisface la funci´on cf, cualquiera que sea la constante c ‚ 0.. También reconocemos el apoyo anterior de la Fundación Nacional de Ciencias bajo las subvenciones números 1246120, 1525057, y 1413739. A menos que se indique lo contrario, el contenido de LibreTexts tiene licencia de CC BY-NC-SA 3.0. Legal. ¿Tiene preguntas o comentarios?

03. Integral doble, teorema de Fubini YouTube
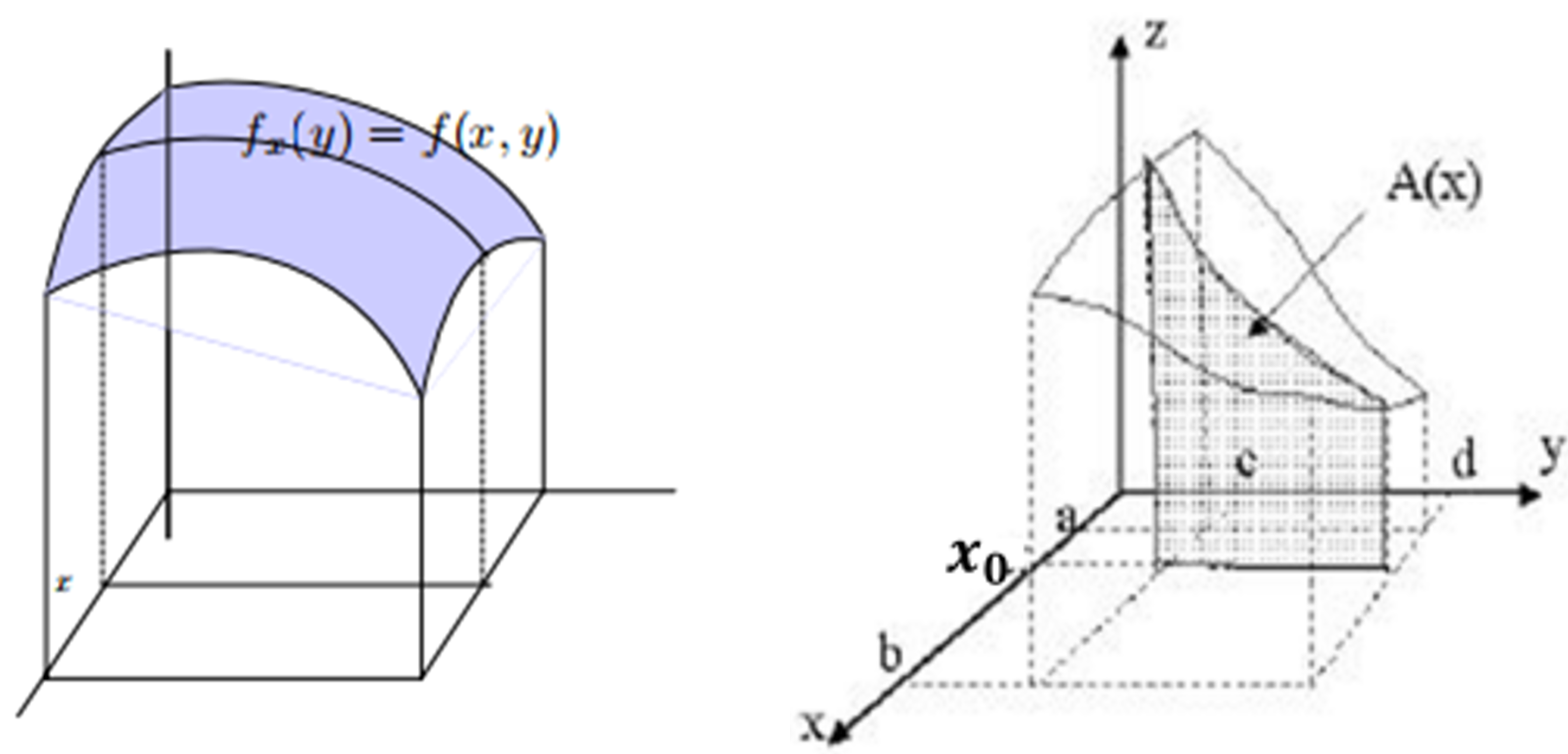
Integrales iteradas, Teorema de Fubini para rectángulos El blog de Leo

Teorema de Fubini e integrais iterados (Exemplo 1) YouTube

Teorema de Fubini YouTube

🎓TEOREMA DE FUBINI CALCULO de INTEGRALES DOBLES 2022 YouTube

15.1.2 Las integrales iteradas, el teorema de Fubini y ejemplos de integrales iteradas resueltos

INTEGRAL TRIPLA 💥 TEOREMA de FUBINI exercícios cálculo2 cálculo3 YouTube

PPT INTEGRALES MULTIPLES Integrales dobles sobre rectàngulos Propiedades Càlculo Teorema de

Teorema de Fubini aplicado a regiones elementales. Integral doble iterada. YouTube

(DOC) AULA 1 INTEGRAL DUPLA TEOREMA DE FUBINI Ariel Fragola Academia.edu

️RESOLVER INTEGRALES👍 DOBLES FÁCILMENTE 💥 PASO A PASO🏆 (TEOREMA DE FUBINI) YouTube
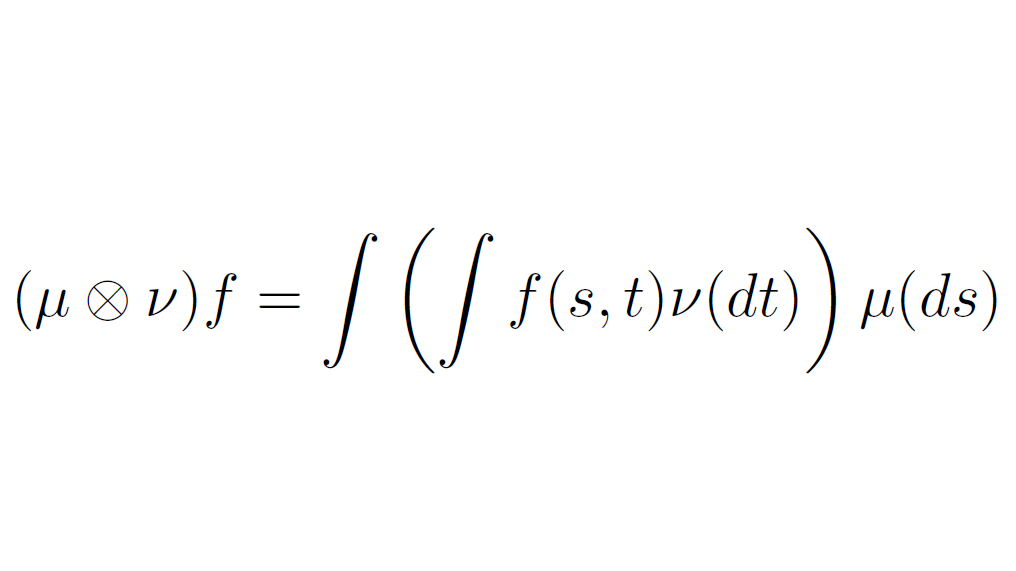
Medidas Producto y Teorema de Fubini

Teorema de Fubini YouTube

Teorema de Fubini YouTube

INTEGRAL DOBLE usando teorema de Fubini, separando como producto YouTube

Measure Theory 19 Fubini's Theorem YouTube

7 1 Teorema de Fubini YouTube

Teorema de Fubini YouTube
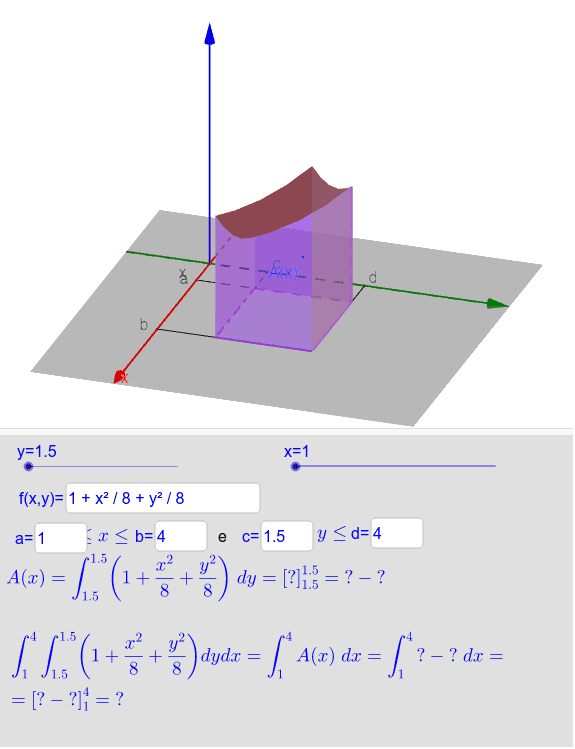
Teorema de Fubini sobre um Retângulo I GeoGebra

Teorema de Fubini para integrales dobles YouTube
Y el teorema de Fubini es comúnmente pensado como el teorema que nos permite intercambiar el orden de integrales iteradas. También podemos obtener el teorema de Fubini aplicando repetidamente nos consigue el siguiente corolario: Let R: = [a1, b1] × [a2, b2] × ⋯ × [an, bn] ⊂ Rn be a closed rectangle and let f: R → R be continuous.. El teorema de Fubini es una herramienta fundamental en el cálculo de integrales dobles. Este teorema establece que la integral doble de una función continua y acotada sobre un rectángulo puede ser calculada de dos formas equivalentes: integrando primero en una variable y luego en la otra, o viceversa. Esto simplifica enormemente el cálculo.